Research

Graduate Research Projects

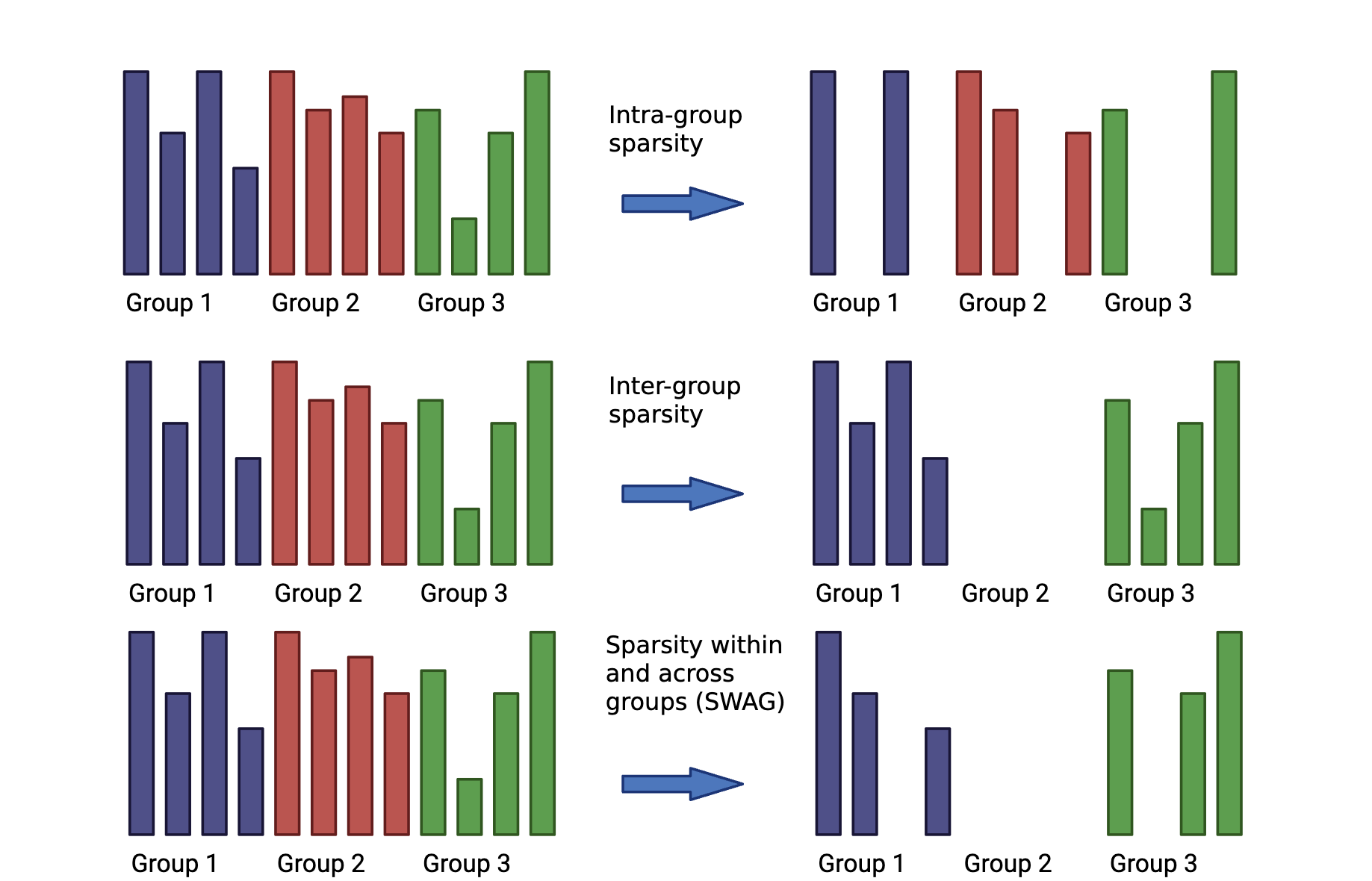
A General Framework for Group Sparsity in Hyperspectral Unmixing Using Endmember Bundles

Gokul Bhusal, Yifei Lou, Cristina Garcia-Cardona, Ekaterina Merkurjev

📄 Paper 💻 Code

Sparsity effect — Effect of sparsity on different models.

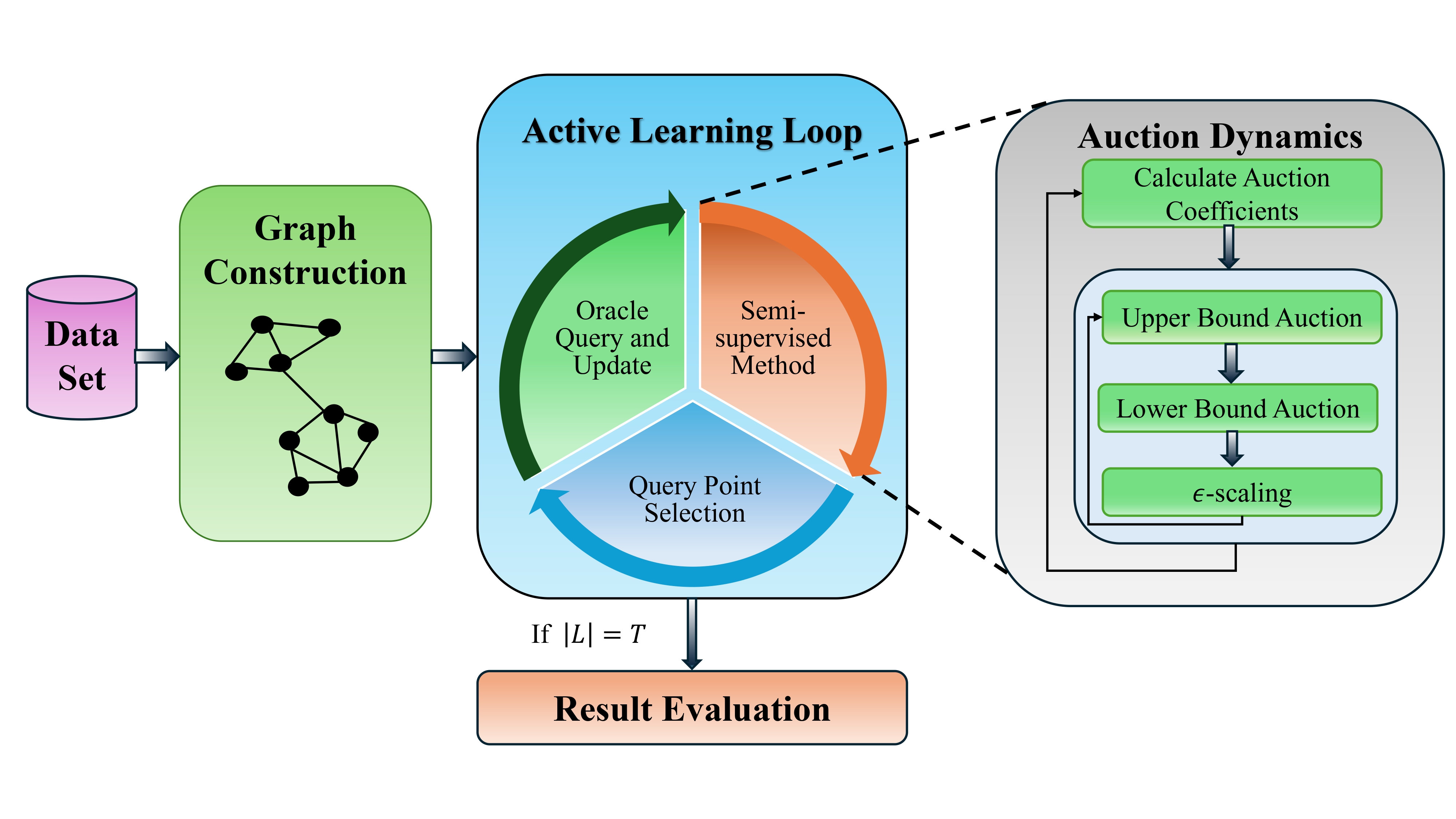
Malady: Multiclass Active Learning with Auction Dynamics on Graphs

Gokul Bhusal, Kevin Miller, Ekaterina Merkurjev

📄 Paper 💻 Code

The flowchart of MALADY framework. — The flowchart of the MALADY framework.

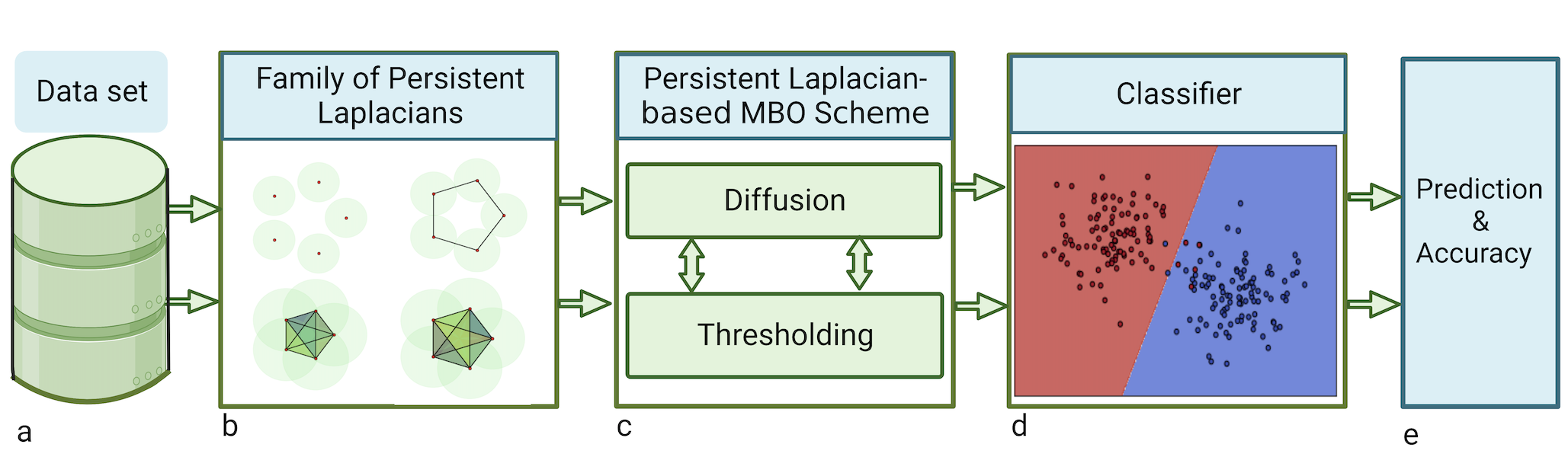
Persistent Laplacian-enhanced Algorithm for Scarcely Labeled Data Classification

Gokul Bhusal, Ekaterina Merkurjev, Guo-Wei Wei

📄 Paper 💻 Code

The flowchart of PL-MBO framework. — The flowchart of the PL-MBO algorithm.

Undergraduate Research Projects

Honors College Thesis: Twisted Central Configurations of the Eight-Body problem

The University of Southern Mississippi, Hattiesburg, MS

I did an honors project advised by Professor Zhifu Xie. We studied twisted central configurations of the eight-body problem, and showed that when the two square configurations share a centroid, a central configuration is possible only if the size ratio falls into one of three intervals. Numerical evidence suggests exactly three nested central configurations exist for each mass ratio.

See my honors thesis

Wright W. and Annie Rea Cross Research: Central configurations in the planar 6-body problem forming two equilateral triangles

The University of Southern Mississippi, Hattiesburg, MS

I was fortunate to receive the Wright W. and Annie Rea Cross Mathematics Undergraduate Research Scholarship. As a cross scholar, I worked with Professor Zhifu Xie and Hamas Tahir on central configurations in six-body systems with equilateral triangles. Detailed numerical analysis revealed nested central configurations and twisted CCs under specific conditions.

See the published paper